
In Problem 55 (Fig. 11–55), the length of the string may be adjusted by moving the pulley. If the hanging mass is fixed at 0.080 kg, how many different standing wave patterns may be achieved by varying between 10 cm and 1.5 m?

In order to watch this solution you need to have a subscription.
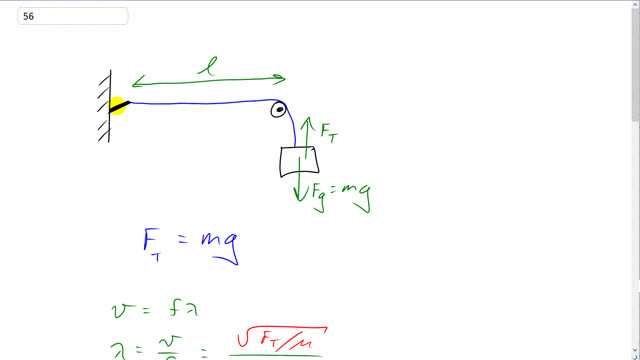
This is Giancoli Answers with Mr. Dychko. We have a mass hanging off the end of this string here. And the mass experiences a weight downwards equal to mg and a tension force upwards. This tension force is going to be the tension in the string and it's going to be equal to the weight of this hanging mass because the mass is not moving. And the string has a length of l that we don't really know what it is, but we know that it can vary from 10 centimeters up to 1.5 meters, and our job is to figure out how many standing wave patterns can fit in between those lengths. We have an oscillator here moving at 60 hertz and it's moving with a small amplitude and that's important because we can still consider this end to be a node. Nodes don't move at all. And now since the oscillator is moving just a little bit, we can still think of it as a node. And let's figure out what the wavelength of this... The wave in the string will be. And then we'll consider this to be a node and this to be a node. And we'll have these standing wave patterns that are possible here. This one is the shortest distance from the pulley to the oscillator possible, and that contains half of a wavelength. And there's a node here and a node there. And then the next smallest possibility would be with this node at the oscillator and then the next node at the pulley being here one full wavelength away from the oscillator. And then we can just guess and check and keep trying the next standing wave pattern here with a node at the weight or pulley and the node at the oscillator here, and that's a wavelength plus half a wavelength. So, that's 3 over 2 wavelengths. And then we'll try this one too and find that it doesn't fit. So, what is the wavelength first of all? Well, we know wave speed is going to be frequency times wavelength. And then we can divide both sides by f and we get wavelength is wave speed divided by frequency. And wave speed is the square root of tension divided by mass per unit length. And the tension we already figured out is mg. So, we'll substitute for that here and I just put this square root μ in the bottom. And so we have wavelength the square root mg divided by frequency times square root mass per unit length. And so that's a square root of 0.08 kilograms times 920 newtons per kilogram divided by 60 hertz times 3.5 times 10 to the minus 4 kilograms per meter square rooted and that gives 0.7888 meters is the wavelength. So, this distance here, l, in the first case will be wavelength divided by 2 and that's going to be 0.394 meters. And so that works because it's greater than 10 centimeters and less than 1.5 meters. And then the next possibility is with this node at the pulley and this node at the oscillator. And that's two antinodes or one full wavelength here. And that's 0.789 and that works. And then the next pattern that's possible is this pattern with l being 3 halves you could say, here's one half wavelength here's another half wavelength, one half, two halves, three halves. And that's 1.18 meters and that works. And then this pattern here which is two full wavelengths does not work because it's 1.578 meters and that exceeds 1.5 and so three standing wave patterns are possible.